植物をつくるときに迷いがちな葉の付き方について、自分なりのベストプラクティスと理由付けをしていく
葉序とは
葉序とは葉の付き方、配列様式です。
※自分は生物学者でもなんでもなく、ただblenderなどで植物を作るときにそれっぽく見せたいという動機で葉序についてメモしております。詳しいことや正しい解説が欲しい方は専門的な記事をお読みください。ここに書いてあることは自分で咀嚼して認識したものです。間違っている可能性があります。

葉の付き方にもいろいろあるらしいですが、中でも知りたいのが互生の螺旋葉序で、葉がつく間の角度を何度にすべきか?という問題です。
blenderで植物を作る場合、大体インスタンスを配置していくときのrotationをどうするかという問題なんですが、ぶっちゃけていうとindexの順番でもランダムでも全然いいと思っています。ただいつも同じ問題で迷ってしまうので、ベストプラクティスを出したい!
葉序が黄金角に近づくとは
現実の植物は葉が日光に当たりやすいよう黄金角(らせん葉序の場合)に近づくようついている種類が多いと言われています。そもそも葉序が黄金角に近づくとはどういうことなのか…
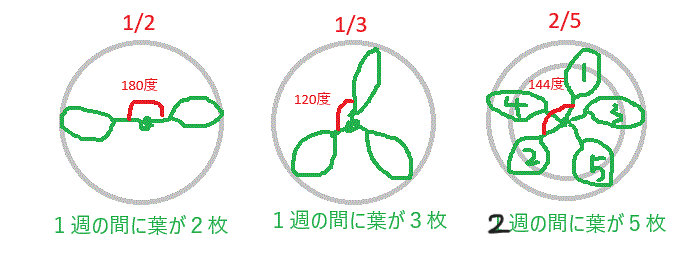
自然の植物を観察すると、葉序が
1/2、1/3、2/5、3/8、5/13、8/21…と
フィボナッチ数列(1、1、2、3、5、8、13、21、…)の一つ飛ばしの分数で現れてるらしいです。なぜフィボナッチ数列に従うのか?ですが、例えば数が大きくなると
89/223 → つまり89週する間に223枚の葉がかぶらない!!たくさんの日光を浴びることができる、やったね!ということじゃないでしょうか。多分そう。
黄金角とは
ではここで黄金角の前に黄金比とはなんだったのかを考えてみます。
黄金比とはフィボナッチ数列(1、1、2、3、5、8、13、21、…)のある項を一つ前の項でわった数が収束していく数。
2÷1 =2
3÷2 =1.5
5÷3 =1.667
…
これを∞項までやると出てくる比率が黄金比1.618…という無理数φです
そして黄金角とは360度を1:φで分割した1側の角度です。数値としては約137.5°らしいです。意外にφ側の角度ではないんですね。

葉序と黄金角のつながり
ではさっきの葉序1/2、1/3、2/5、3/8、5/13、8/21…
とフィボナッチ数列1、1、2、3、5、8、13、21、…
と黄金角360×1÷(1+φ)のつながりなんですが、
例えば葉序2/5のとき、角度を出す計算は360×2/5となります。この2/5の葉序の部分が黄金角を出すときの1/(1+φ)に収束していくという話なんですね。
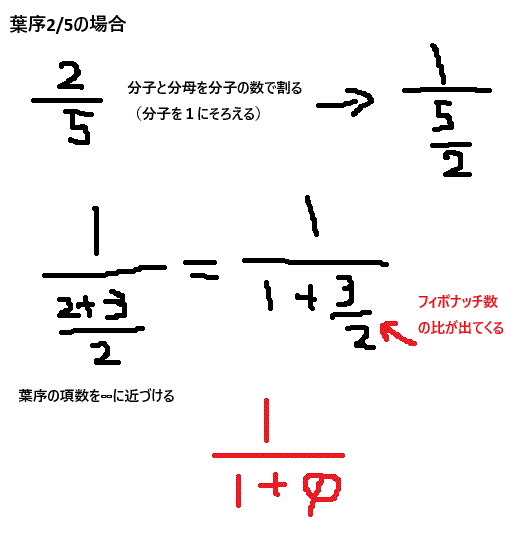
ここで上の図のように分子の数を1に合わせると分母にフィボナッチ数がでてくるようになります。この葉序の項数を∞に近づけると(lim n → ∞)さきほどの黄金角を出した比が出てきます。ここで葉序と黄金角、フィボナッチ数、黄金比が全てつながりました!!
そもそも∞枚の葉っぱがついてる植物なんてないけれど、これでもし、∞枚葉がついていてもどの葉っぱも日光に浴びることができる機能性抜群の植物を作ることが可能です!
blenderでの実装

葉の付き方をrotate Instanceで回転させています。ここで元の数値としてindexを参照しています。ここで入る数値はラジアンなので、indexで0,1,2,3…と入っていくと1ラジアン(約57.3°)入ってしまっているので、黄金角約137.5°を1ラジアン分の約57.3°で割った比率をかけると、インデックス順に黄金角の葉序で葉っぱをつけることができます。葉が少なくても多くてもバランスよく葉を配置できるのでとても便利な数値になるかと思います。でもめんどいから2.4かけちゃってもいいかも。
一応他の数値もみておきます。

これはただのindex番号をラジアンとしていれているだけです。57°くらいの間隔なので詰まってる感じになりますね。葉の枚数によってはバランスが悪くなるかもしれません
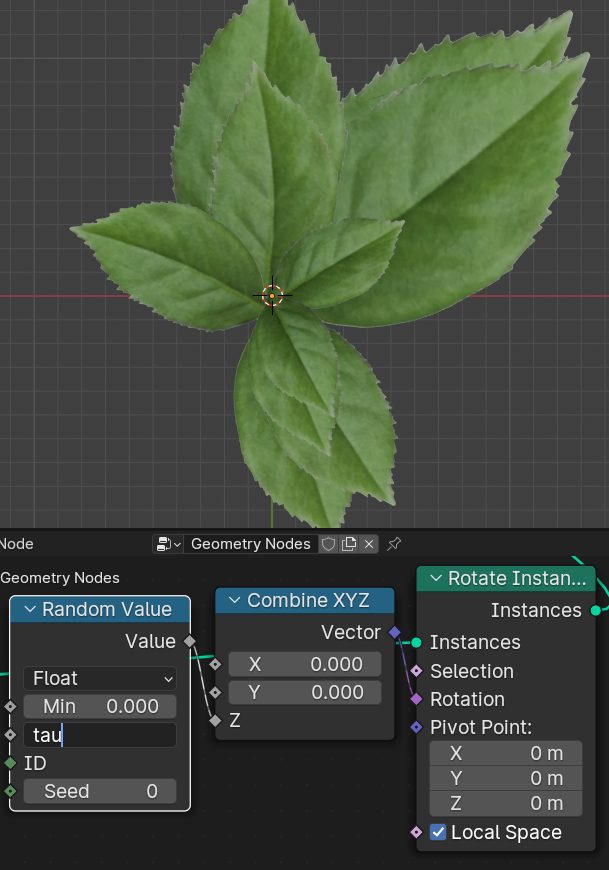
これはランダムです。数値は0~tau(360°)をいれています。かなり重なっていてバランスが悪いです。
とは言っても自然界にはこの機序がなかったり、ずれたり、いろいろな植物がありますので、好きなようにすればいいと思います。葉の大きさも線形ではなく二次か三次曲線のようになっていた方がいいからとスケールするときにeを累乗したりする方もいらっしゃいますが、自分はここまで考えるともう何も作れなくなるような気がするのでできればこういうことは無視する胆力を身に着けたいとおもっています。
でも3DCGをやっていると、このようないろいろな計算や自然の不思議さに触れることができておもしろいと日々実感します。これらのようなことも造形の楽しさの一環として、今後も(できる範囲で)自然や物理や数学の面白さを発見していきたいです。



